コレクション 図形 の 求め 方 868273-図形 の 重心 の 求め 方
図形の求め方 数学 Xの求め方を教えてください 三角形の内角の和よ Yahoo 知恵袋
図に示された円は、直径 4 の円ですね。 半径 r は、直径の半分より、 r = 4 2 = 2 r = 4 2 = 2 です。 あとは公式に代入して S = πr2 = π× 22 = 4π S = π r 2 = π × 2 2 = 4 π 小学生向けに、円周率 π を 314 として計算すれば 円の面積 = 半径× 半径×314 = 2 ×2× 314 = 1256 円の面積 = 半径 × 半径 × 314 = 2 × 2 × 314 = 1256 となります。半径 r、高さ h の円柱 底面の半径 r r 、高さ h h の円柱の表面積 S S は、次の式で求められます。 円柱の表面積 V = 2πr2 2πrh V = 2 π r 2 2 π r h 表面積 = 2 × 半径 × 半径 × 314 直径 × 314 × 高さ 公式の導出方法と計算例については、「 円柱の表面積の求め方 」をご覧ください。
図形 の 重心 の 求め 方
図形 の 重心 の 求め 方-イメージ内の円形オブジェクトの中心と半径を推定し、この情報を使用して円をイメージ上にプロットします。 この例では、 regionprops は測定した領域プロパティを table で返します。 イメージをワークスペースに読み取ります。 a = imread ( 'circlesBrightDarkpng中3相似中点連結定理、三等分の三角形求め方を問題解説! 相似な図形 中3数学相似な図形の見つけ方、相似条件とは?
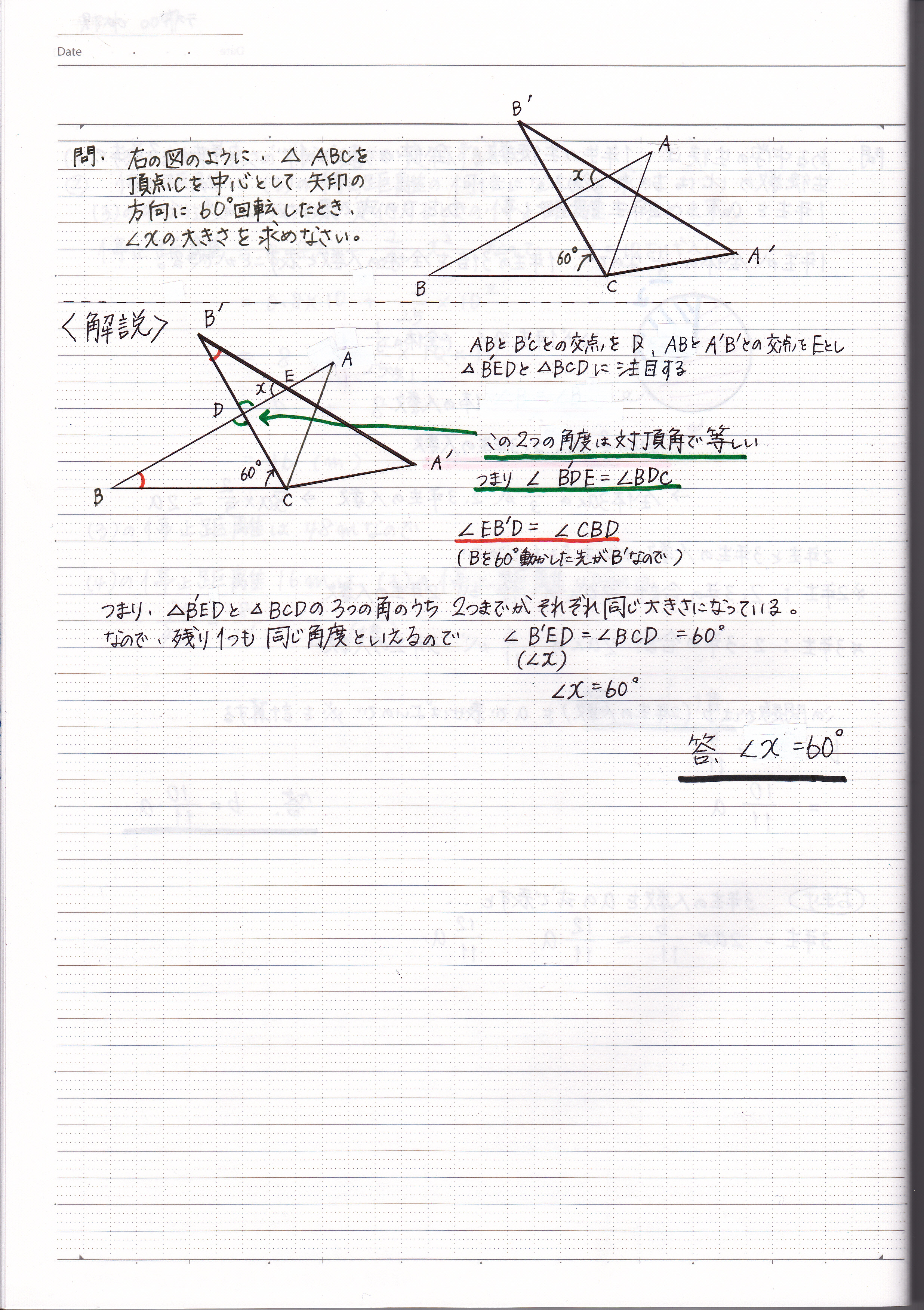
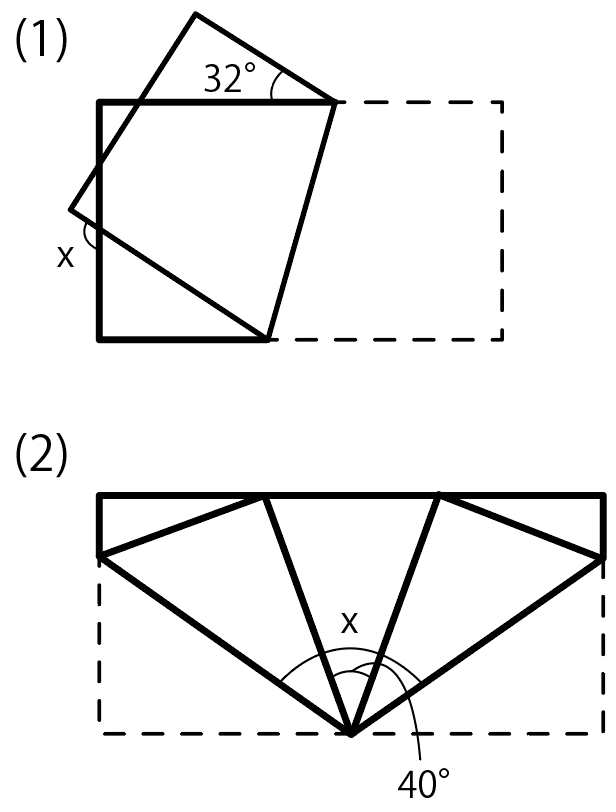
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
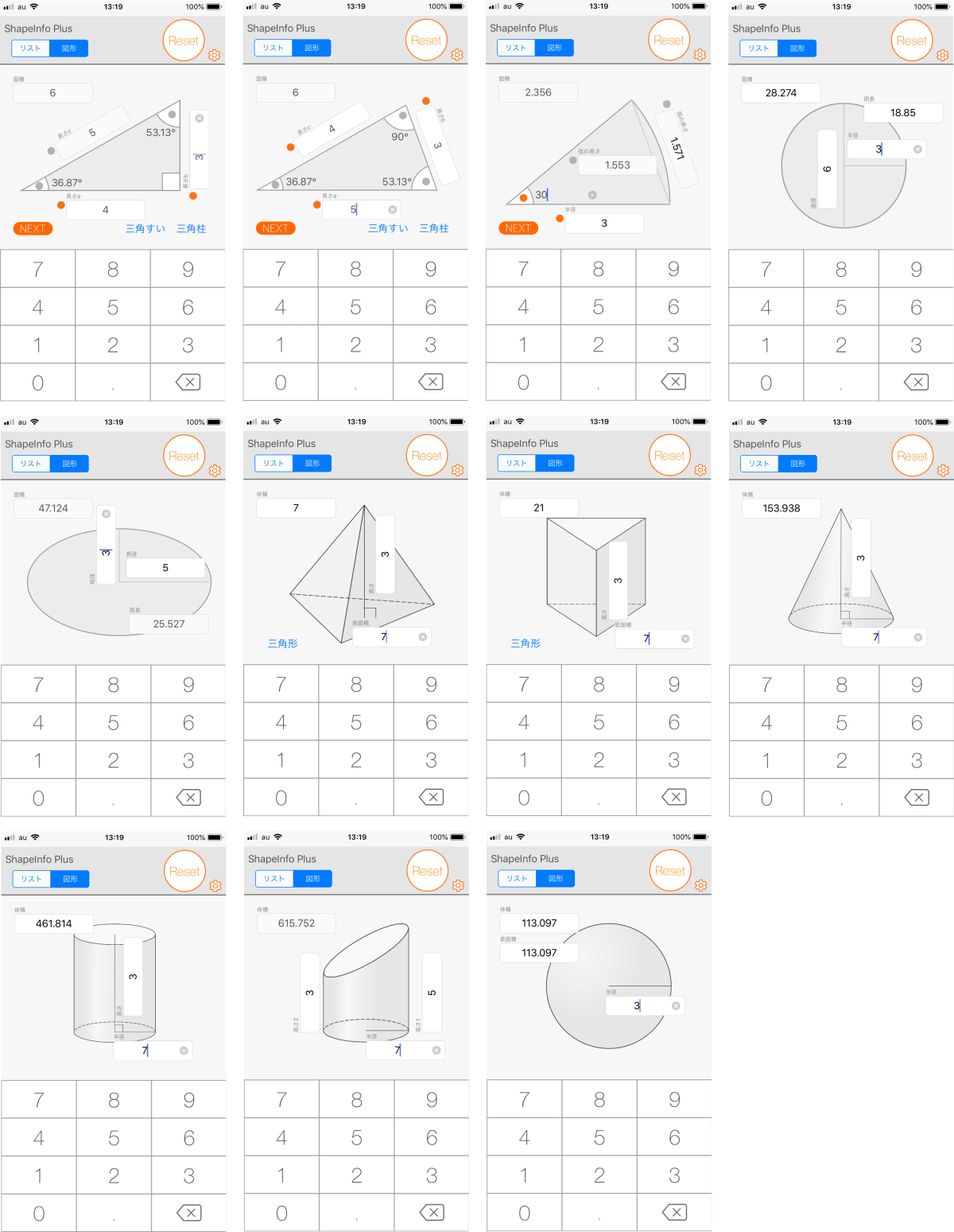
空間図形 表面積や体積の求め方のポイントです。 代表的な三角柱,四角柱,円柱,球や半球などを取り上げて説明しますが、公式ではなく、求めるための手順を覚えるようにしましょう。 問題には公式が使えない立体が多く出てきますので、覚えることを間違えないようにしてください。図形と計量180°θの三角比 「数学」のQ&Aをすべて見る 全体のQ&Aランキング 動名詞①構文の訳し方②間接疑問文における疑問詞の訳し方 数列Σの和の求め方 関数と極限∞+∞=∞とは 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360
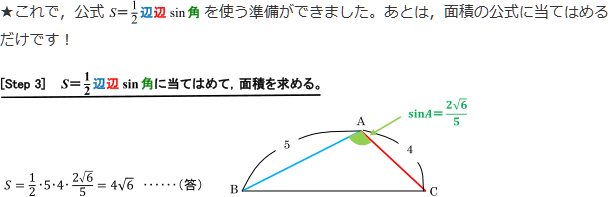
三角形、四角形、角、面積 円、三角形、四角形の面積を計算できるようになろう。 角度のはかり方もいっしょにおぼえてね。 動画で学ぼう! (NHK for School) 三角形の面積の求め方を、四角に直すことで原理から考える。 結婚式場から指輪が盗まれた三辺の長さが a、b、c の三角形 三辺の長さ a,b,c a, b, c の三角形の面積 S S は、次のヘロンの公式で求められます。 三角形の面積(ヘロンの公式) S = √s(s −a)(s− b)(s− c) ただし s = a b c 2 S = s ( s − a) ( s − b) ( s − c) ただし s = a b c 2 公式の 導出 星型など複雑な図形の角の和を求めるとき、三角形の外角の定理や、ブーメラン型四角形の角、リボン型(ちょうちょ型)の三角形の角の考え方が役立ちます。 角の和の例題と解き方を紹介しますので、どう解いたらいいかわからないという人は参考にしてみてください。 1 多角形の角の和考え方の基本 2 多角形の角の和応用問題の考え方 21 星型タイプ
図形 の 重心 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 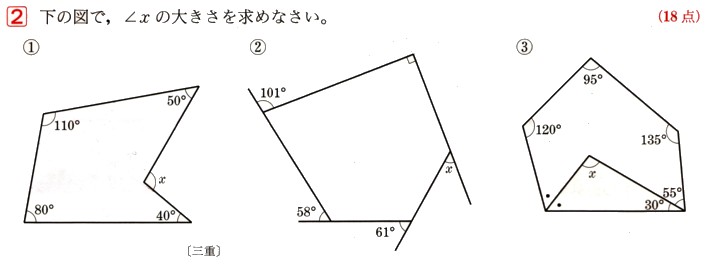 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 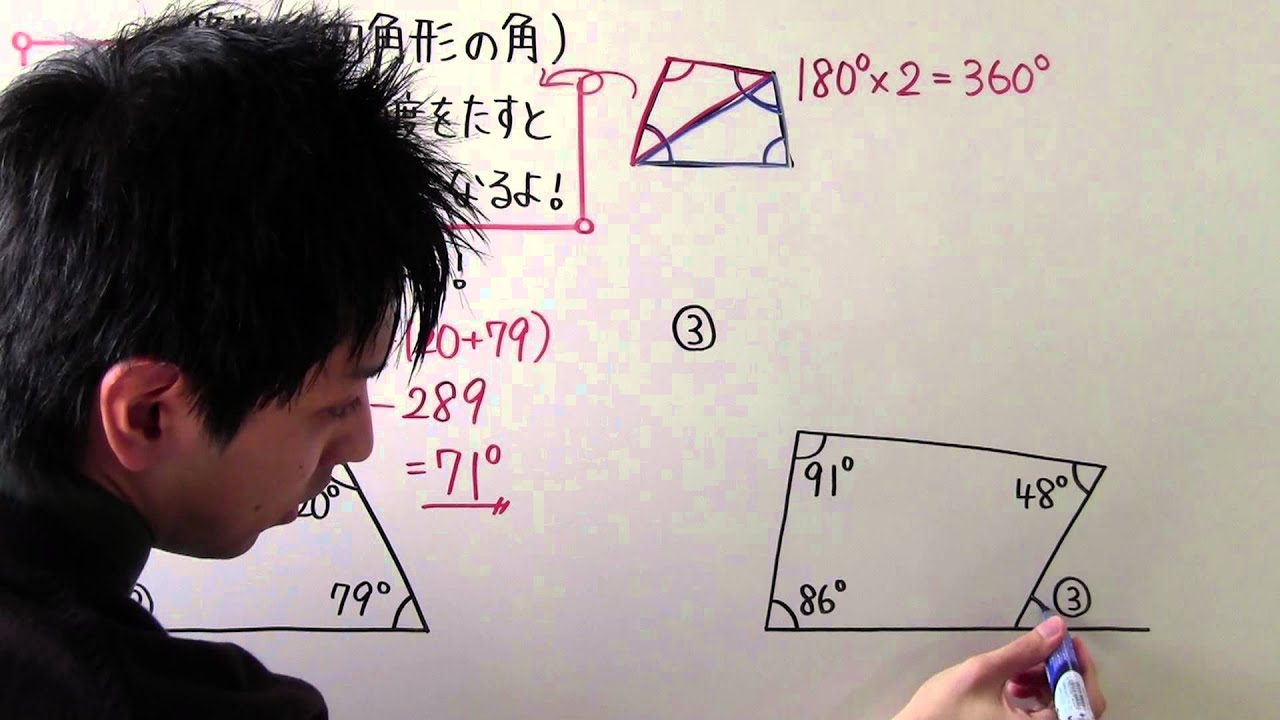 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 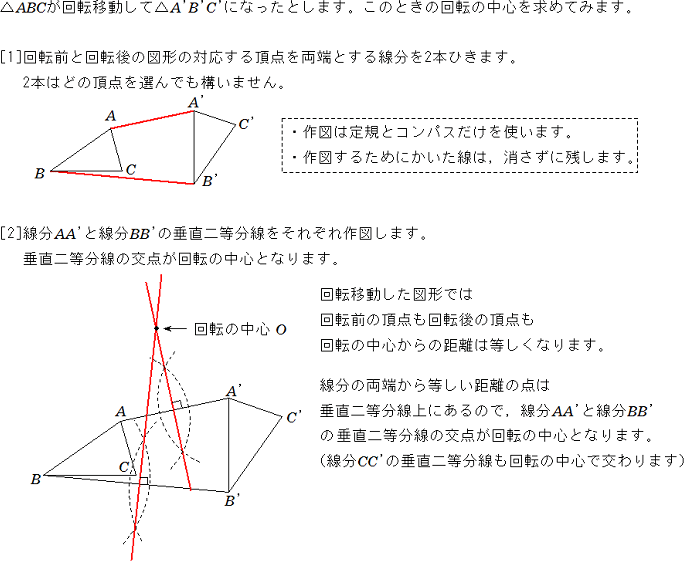 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 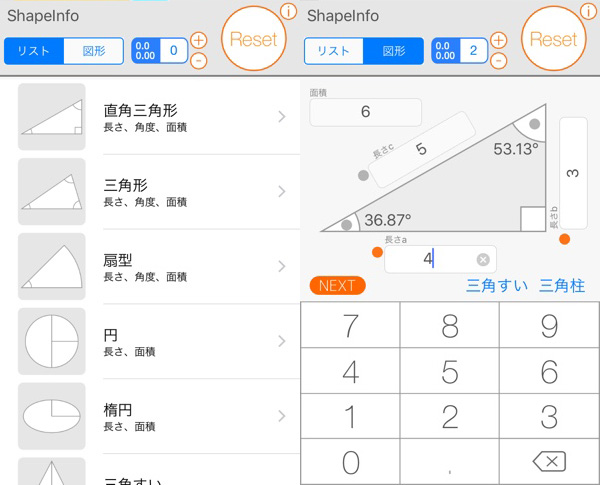 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 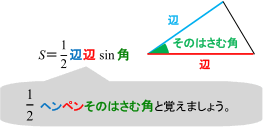 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 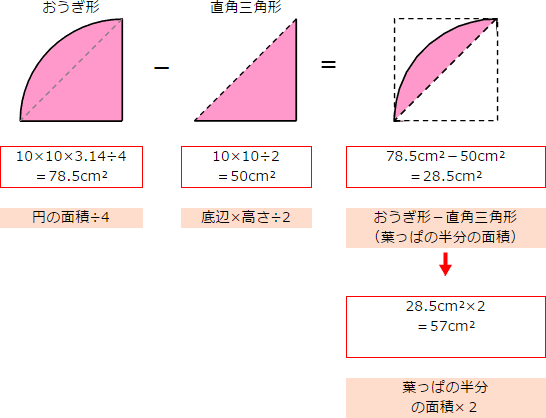 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 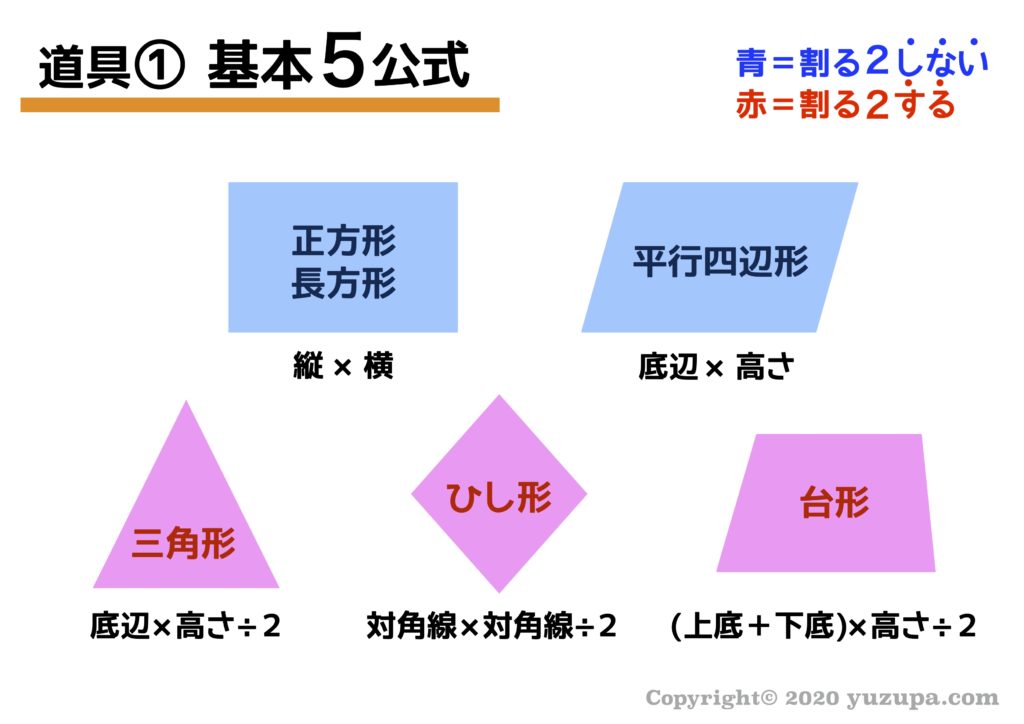 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 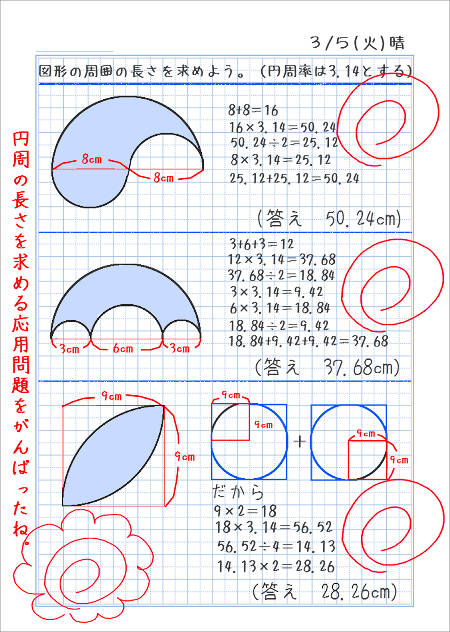 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |  扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ | 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ |
底面の半径 $r$、高さ $h$ の円錐の体積 $V$ は、次の式で求められます。 円錐 (えんすい) の体積 \begin{align*} V = \frac{1}{3} \pi r^2 h \end{align*} 体積 = 半径 × 半径 × 314 × 高さ ÷ 3 公式の 導出 (どうしゅつ) 方法と計算例は、「円錐の体積の求め方」をご覧ください。まず、外角1つ分の大きさを求めて 180°から外角1つ分の大きさを引いてやります。 先ほど外角の求め方のところで 1°になるということがわかっているので 正三角形の内角1つ分の大きさは $$\large{1801=60°}$$ となります。 正五角形の場合
Incoming Term: 図形 の 重心 の 求め 方,
コメント
コメントを投稿