[無料ダウンロード! √] reflection across y=x 337581-Reflection across y x+2
ΔDEF with D (4,1), E (0,10) and F (1, 1) is reflected across the line y = x Which of the following are the correct coordinates for ΔD'E'F' answer choices D' (1, 4) E' (10, 0) F' (1, 1) D' (1, 4) E' (10, 0) F' (1, 1) D' (1, 4) E' (10, 0) F' (1, 1) D' (1, 4) E' (10, 0) F' (1, 1) s Reflection in the coordinate plane is based on whether the reflection is over \(X\)axis, \(Y\)axis and in the origin \(\left( {0,\,0} \right)\) Reflection over X axis The \(x\)coordinate remains the same when a point is reflected across the \(x\)axis, while the \(y\)coordinate is turned into the opposite (its sign is changed) 👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the x
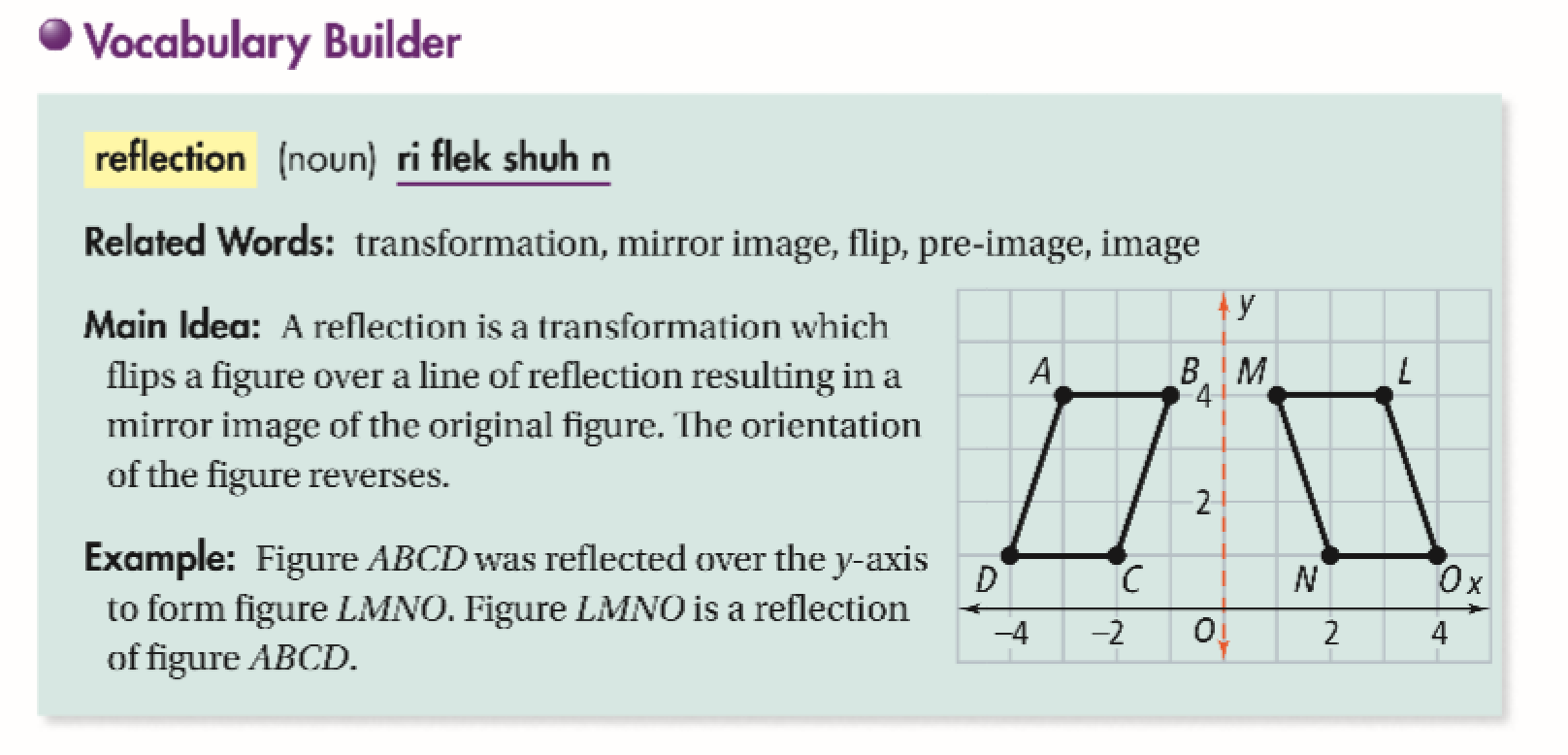
Reflections Bright Star Schools
Reflection across y x+2
Reflection across y x+2- Answer You could plot the point and work out the answer quite rapidly I'll do this and the matrix method If we reflect (4,3) across y axis, the point becomes (4,3) if you visualise it When we reflect this in the 'x' axis, we get (4,3), if you visualise it This is a lot faster than the From the diagram we see the object point ( − 2, −5) is mapped to (x',y') by a reflection in the line X = 2 we note (1) the ycoordinate is unaffected (2) for reflections the distance from the line of reflection to the object is equal to the distance to the image point ∴ a = 2 2 = 4units so the image point is 4 units from the line of




4 2 Reflections Warm Up Maintaining Mathematical Proficiency Find The Measure Of Each Variable Justify Your Solution Ppt Download
Reflection across y= x 1 See answer savannahtyler843 is waiting for your help Add your answer and earn points absor1 absor1 Answer option A) is correct Stepbystep explanation As we know that when we reflect across the line , the xcoordinate and ycoordinate would change places and be negatedLearn termreflection rotation = (x,y)=( x, y) with free interactive flashcards Choose from 500 different sets of termreflection rotation = (x,y)=( x, y) flashcards on QuizletApply a reflection over the line x=3 Since the line of reflection is no longer the xaxis or the yaxis, we cannot simply negate the x or yvalues This is a different form of the transformation Let's work with point A first Since it will be a horizontal reflection, where the reflection is over x=3, we first need to determine the distance of the xvalue of point A to the line of reflection
How To Given a function, reflect the graph both vertically and horizontally Multiply all outputs by –1 for a vertical reflection The new graph is a reflection of the original graph about the xaxisReflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinatesThe reflection of point (x, y) across the xaxis is (x, y) When you reflect a point across the yaxis, the ycoordinate remains the same, but the xcoordinate is taken to be the additive inverse The reflection of point (x, y) across the yaxis is (x, y) Learn what it means to bring Yup to your school or district
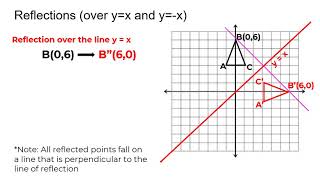
90˚ counterclockwise rotation about the origin OR 270˚ clockwise rotation about the origin Which rigid motion maps A(3, 1) to A'(3, 1)?A Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The image below shows a general Cartesian coordinate being reflected in the line y = −xWhen reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x =(y,x) For example For triangle ABC with coordinate points A(3,3), B(2,1), and C(6,2), apply a reflection over the line y=x By following the notation, we would swap the xvalue and the yvalue



Solved Graph The Image Of The Figure Using The Chegg Com



Reflections Over The X Axis And Y Axis Explained Youtube
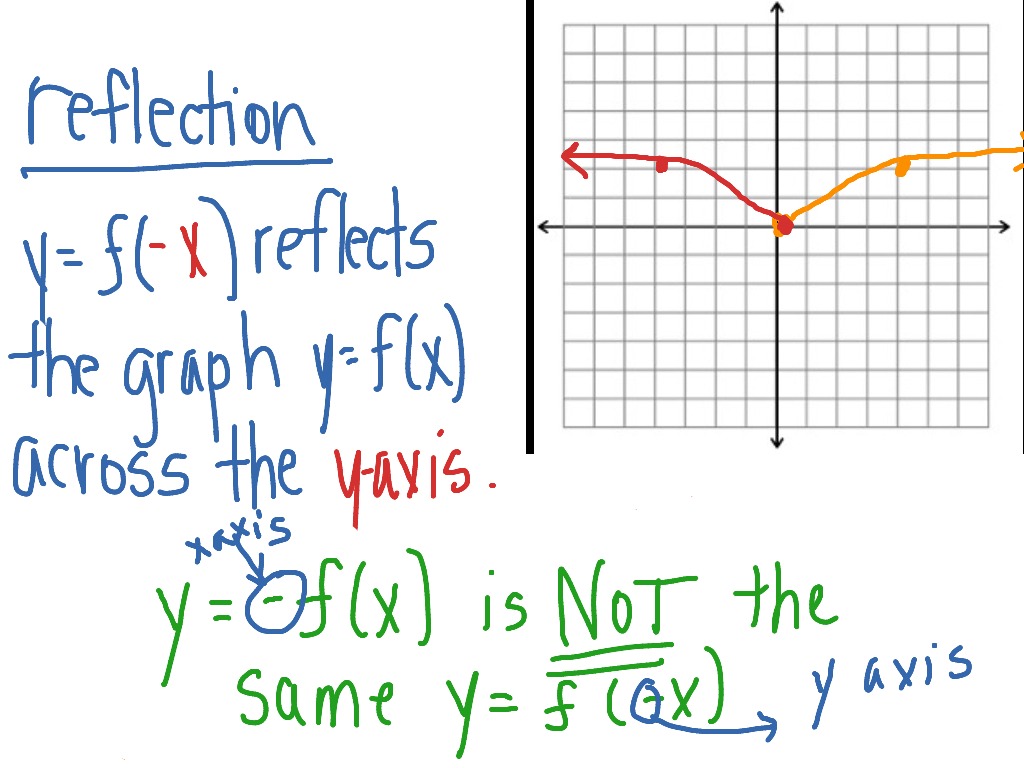
Reflection across the yaxis y = f ( − x) y = f (x) y = f ( − x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versa Basic ConceptsX y K I H I' H' K' reflection across x = −2 12) x y G X F X' F' G' reflection across the yaxis 13) x y N Z X Z' X' N' reflection across x = −2 14) x y U B M S M' B' S' U' reflection across x = 22Create your own worksheets like this one with Infinite PreAlgebra Free trial available at KutaSoftwarecom Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versa




Transformations Boundless Algebra



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
180˚ rotation about the origin (clockwise or counterclockwise would give you the same result)Graphing Reflections In addition to shifting, compressing, and stretching a graph, we can also reflect it about the xaxis or the yaxisWhen we multiply the parent function latexf\left(x\right)={b}^{x}/latex by –1, we get a reflection about the xaxisWhen we multiply the input by –1, we get a reflection about the yaxisFor example, if we begin by graphing the parentA reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6)




Reflections Ck 12 Foundation



Does Reflecting The Parabola Across The X Axis Change The Axis Of Symmetry Quora
A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection y = −x Homework Statement Let T R 2 →R 2, be the matrix operator for reflection across the line L y = x a Find the standard matrix T by finding T(e1) and T(e2) b Find a nonzero vector x such that T(x) = x c Find a vector in the domain of T for which T(x,y) = (3,5) Homework Equations The Attempt at a SolutionSummary Reflections and Rotations Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)




Reflection Mathbitsnotebook A1 Ccss Math
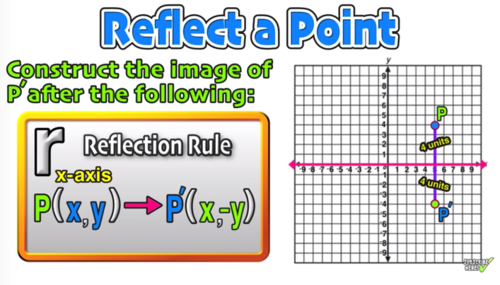



Reflection Over The X And Y Axis The Complete Guide Mashup Math
Reflection Across Y=X Reflection Across Y=X How do you graph a reflection?Answer (1 of 2) There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joining PP′ is perpendicular to Reflections Activity The first 8 boxes have all positive coordinates and students reflect over the x axis, y axis, y =x, over the origin, and over lines (y = 2, x= 2) The second set of 8 boxes have positive and negative coordinates Great pairs activity Have students complete a box with a partner then change partne




Reflections Geometry Abroad




Reflection Transformation Matrix
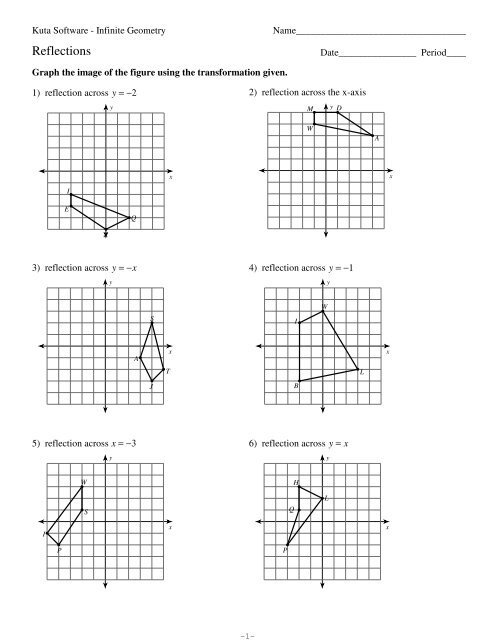
1) reflection across the yaxis x y W EC M 2) reflection across the xaxis x y X W I 3) reflection across the yaxis x y B S Z 4) reflection across the xaxis x y T R I 5) reflection across the yaxis x yReflection over yaxis (x, y) (x, y) Reflection over xaxis (x, y) (x, y) Reflection over line y = x (x, y) (y, x)The Reflection upon the YAxis As the contrary case of XAxis, the YAxis here will stay the same while the Xcoordinates transform with their opposite symbols when the reflection takes place across the YAxis (Image to be added soon) (Image to be added soon) Therefore, X, Y is the reflection of point and is changed as X, Y in the




Reflection Across The X Axis Reflection Math Chart




Pearson Unit 2 Topic 8 Transformational Geometry 8 2 Reflections Pearson Texas Geometry C 16 Holt Geometry Texas C Ppt Download
Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlpha Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



Showmethemath Com




Introduction And Review Information Ppt Video Online Download
Reflection across the yaxis y = f ( − x ) y = f (x) y=f (−x) Besides translations, another kind of transformation of function is called reflection If a reflection is about the yaxis, then, the points on the right side of the yaxis gets to the right side of the yaxis, and vice versaWe can reflect the graph of y=f(x) over the xaxis by graphing y=f(x) and over the yaxis by graphing y=f(x) See this in action and understand why it happensStep 1 First we have to write the vertices of the given triangle ABC in matrix form as given below Step 2 Since the triangle ABC is reflected about xaxis, to get the reflected image, we have to multiply the above matrix by the matrix given below Step 3
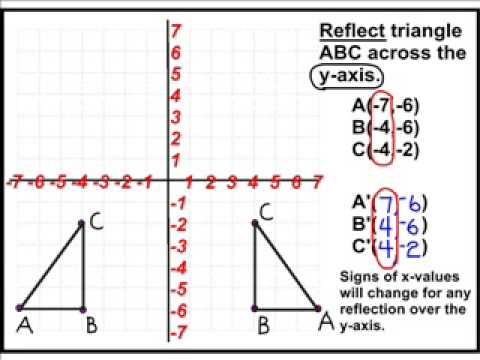



Transformations Reflection Youtube



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
Graph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the yA reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $Reflection over the line y=x reflection over yaxis Reflection over y=x is over of equals percent over 100 reflect over x= 1 You must be logged into ShowMe Signup




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflections Across Y X Geogebra
Reflection over the yaxis f (x) reflects f (x) over the yaxis Horizontal Reflection Reflections are mirror images Think of "folding" the graph over the yaxis On a grid, you used the formula (x,y) → (x,y) for a reflection in the yaxis, where the xvalues were negated Keeping in mind thatThe reflection of the point ( x,y) across the xaxis is the point ( x,y ) Reflect over the yaxis When you reflect a point across the y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite (its sign is changed) Notice that B is 5 horizontal units to the right of the y axis, and B' is 5 horizontal units to the left of the y axisThe sign of describes the reflection across the xaxis means the graph is reflected across the xaxis Reflection about the xaxis None The value of describes the vertical stretch or compression of the graph is a vertical stretch (makes it narrower) is a vertical compression (makes it wider)



Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis



1
Reflection over x axis and y axis When P(x, y) is reflected in the mirror line to become p'(x', y'), the mirror line perpendicularly bisects pp' Thus, for every point of an object, the mirror line is perpendicularly bisects the line segment joining the point with its imageReflection over the line y = x Which rigid motion maps A(3, 1) to A'(1, 3)?The reflection transformation may be in reference to X and Yaxis Reflection over Xaxis When a point is reflected across the Xaxis, the xcoordinates remain the same But the Ycoordinates are transformed into its opposite signs Therefore, the reflection of the point (x, y) across Xaxis is (x, y)
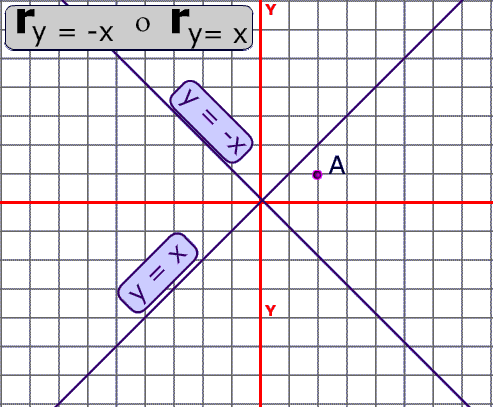



Compositions Of Reflections In Mathematics Theorems Involving Parallel And Intersecting Lines Interactive




Reflection Mathbitsnotebook A1 Ccss Math
Reflecting a quadrilateral over the xaxis If you're seeing this message, it means we're having trouble loading external resources on our website If you're behind a web filter, please make sure that the domains *kastaticorg and *kasandboxorg are unblockedThe rule for a reflection in the line y = x is ( x , y ) → ( y , x ) Reflection in the line y = − x A reflection of a point over the line y = − x is shownReflection across the y axis Reflection across the y axis Log InorSign Up f x = x − 3 3 − x 5 1 − f x 2 f − x 3 − f




Reflection Mathbitsnotebook A1 Ccss Math




Reflection In The Line Y X Geogebra
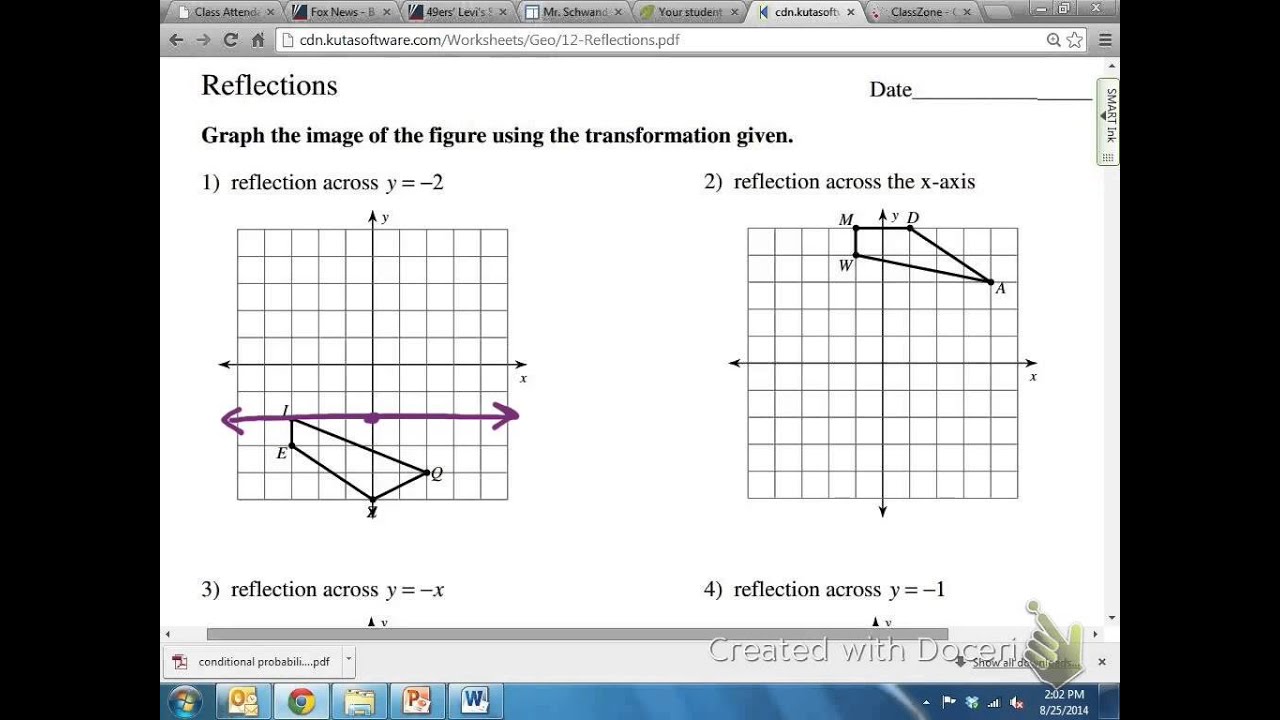



Common Core Math Geometric Reflection Over Y 2 Youtube




Reflection Rules How To W 25 Step By Step Examples
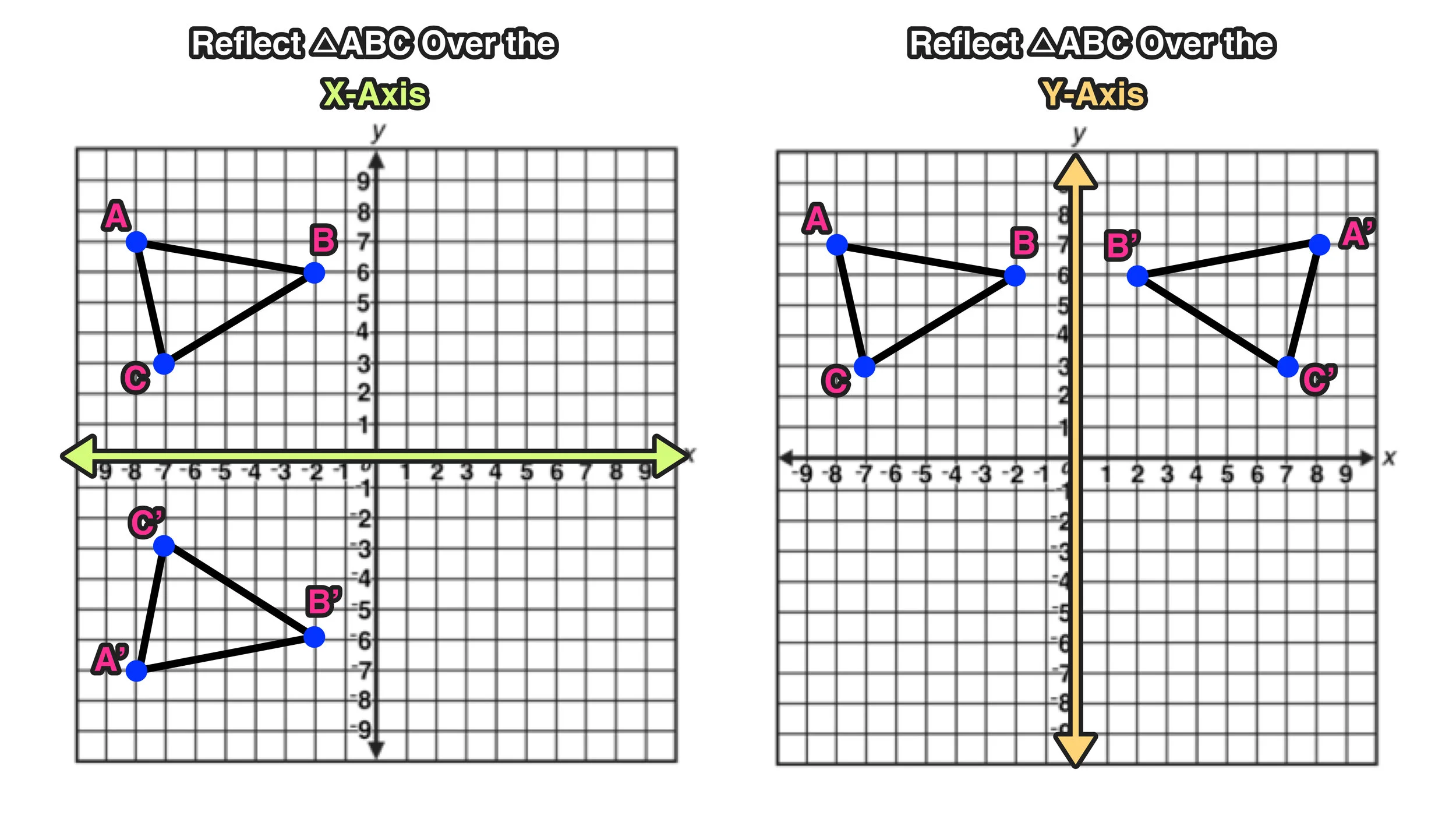



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Transformations Of Graphs
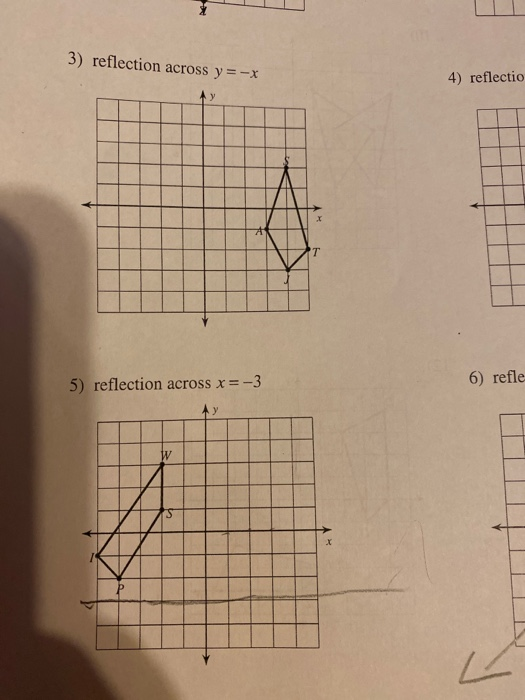



Solved 3 Reflection Across Y X 4 Reflectio 5 Chegg Com




Reflection Across Y X Brainly Com




Reflection Rules How To W 25 Step By Step Examples




Describe The Transformation A Reflection Across The X Axis B Reflection Across The Y Axis C Brainly Com
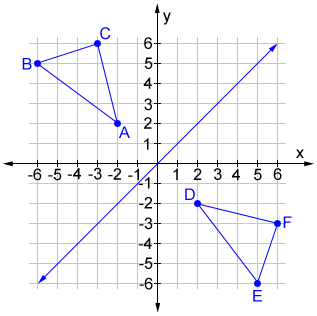



Reflection




How To Find A Reflection Image




Geometry Reflection Across Y X Youtube



What Is The Image Of 2 5 Reflected Across X 2 Socratic




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




A Translation X Y X 5 Y Reflection Across Y Axis B Translation X Y X Y 5 Brainly Com




In The Xy Coordinate Plane Point P Is The Reflection Of The Point With Coordinates 3 1 Across The Line Y X Point T Is The Reflection Of Point P Across The Y Axis What
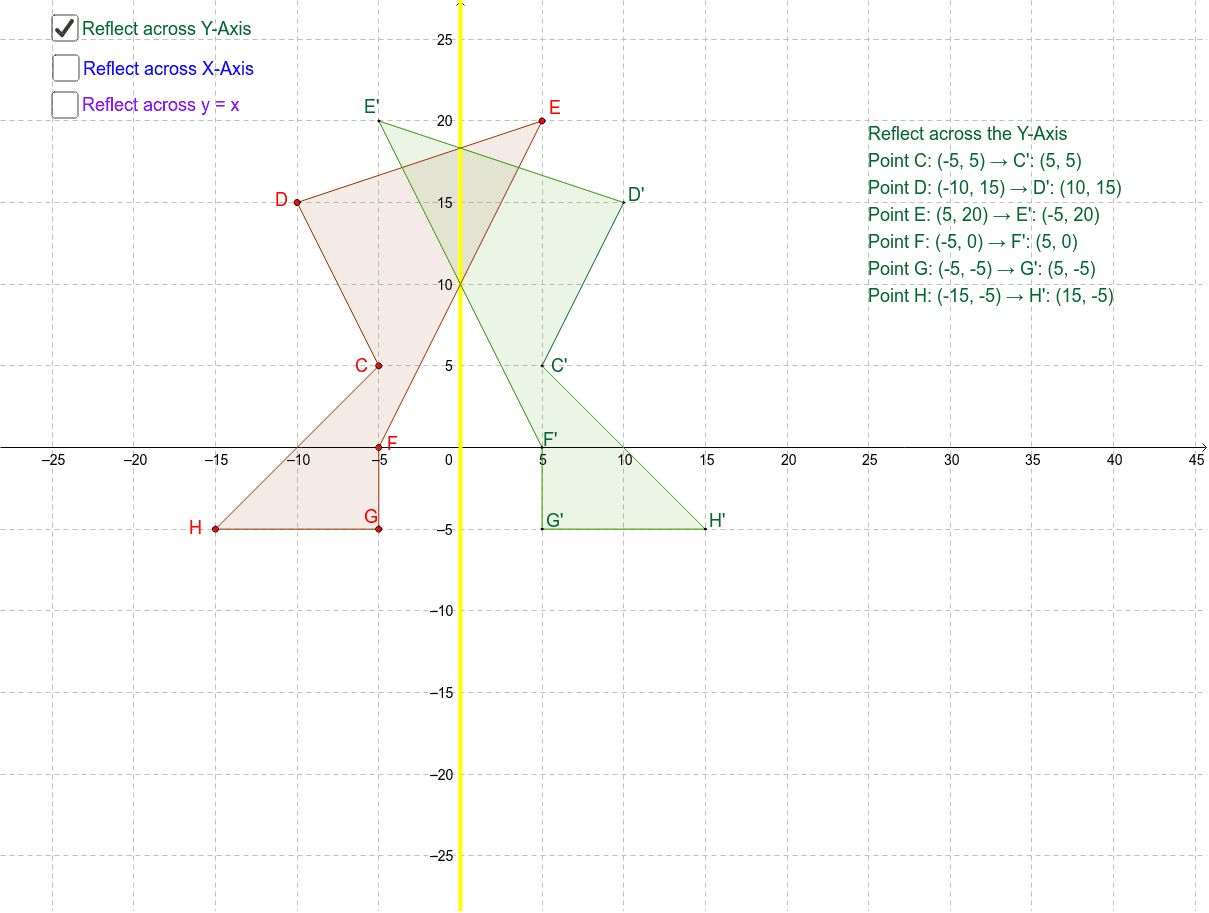



Reflections Across Axes And Y X Geogebra



1




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



Math Practice Problems Transformations 2




Transformation Rules Flashcards Quizlet




Reflection Over Y X Math Geometry Showme



Reflection Across X 1
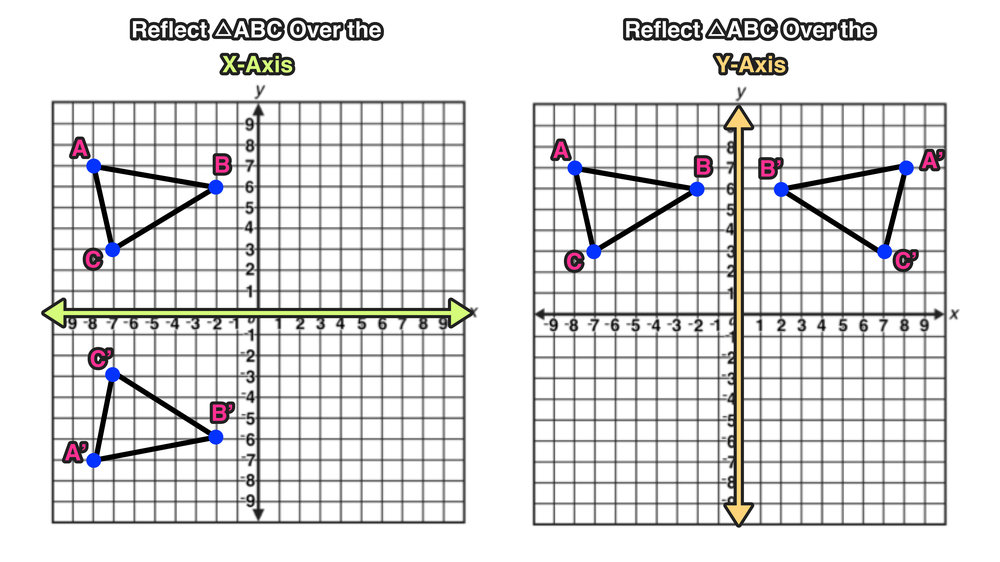



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Rules How To W 25 Step By Step Examples



5 7 Proofs Using Coordinate Geometry
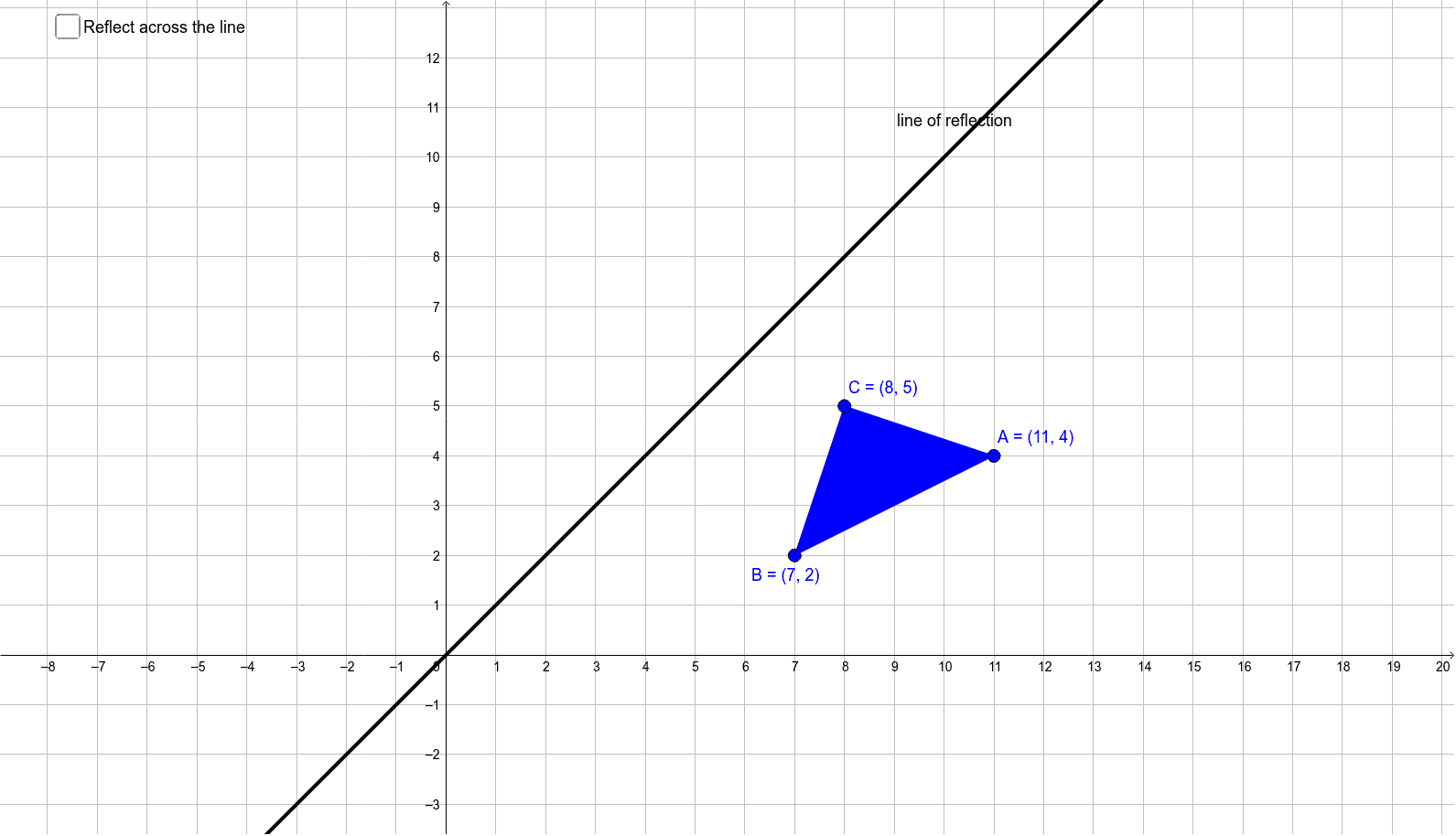



Reflection Across Y X Geogebra



Ms Sobon S Math Connections To The World 9 Fri Reflections Across The Y Axis




How To Find A Reflection Image
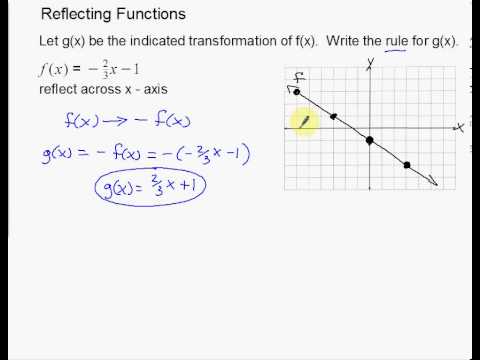



Linear Reflections Across X And Y Axis Example Youtube




Transformation Reflection Over The Line Y X Youtube




Reflection Mathbitsnotebook A1 Ccss Math



What Does It Mean To Reflect Over The Y X Line Quora




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
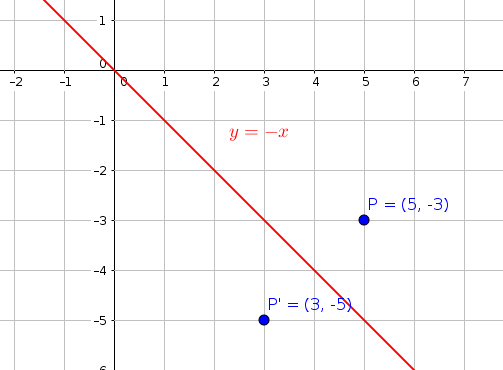



What Is The Reflection Image Of 5 3 In The Line Y X Socratic
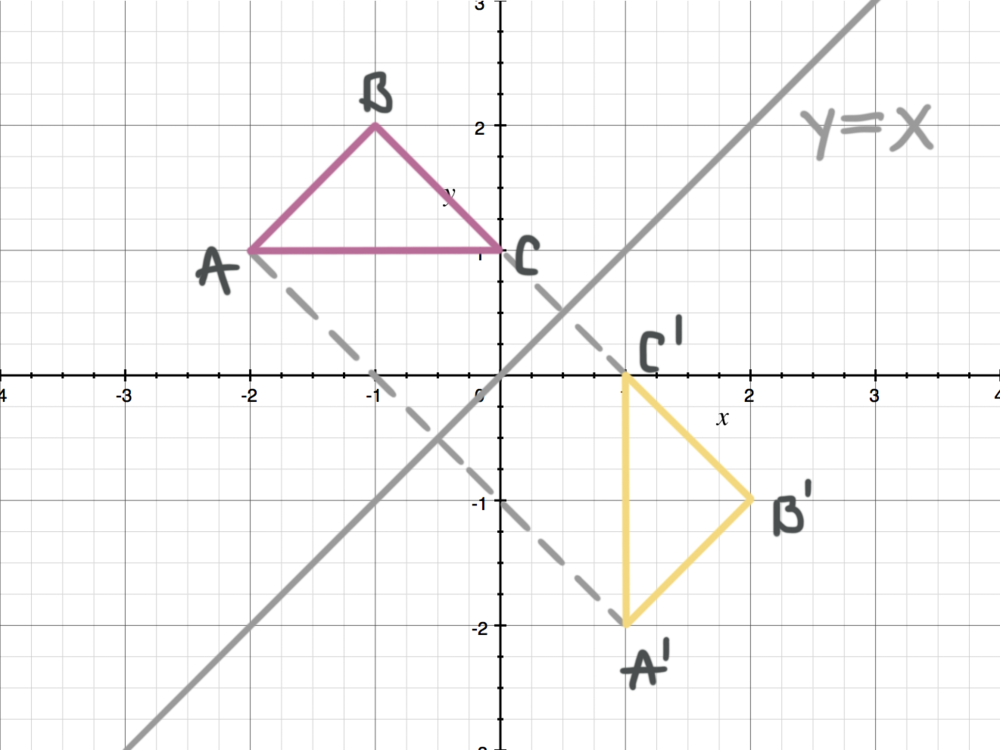



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics




What Series Of Transformations From Abc To Def Shows That Abc Def A A Reflection Across Brainly Com




Reflection Over The Y X Line Youtube
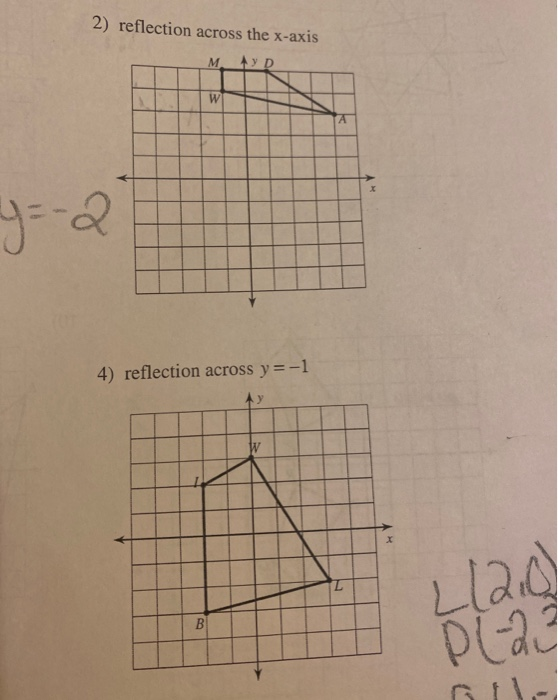



Solved 2 Reflection Across The X Axis Mayd 4 Reflection Chegg Com




Learn About Reflection Over The Line Y X Caddell Prep Online




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflecting Shapes Video Reflections Khan Academy
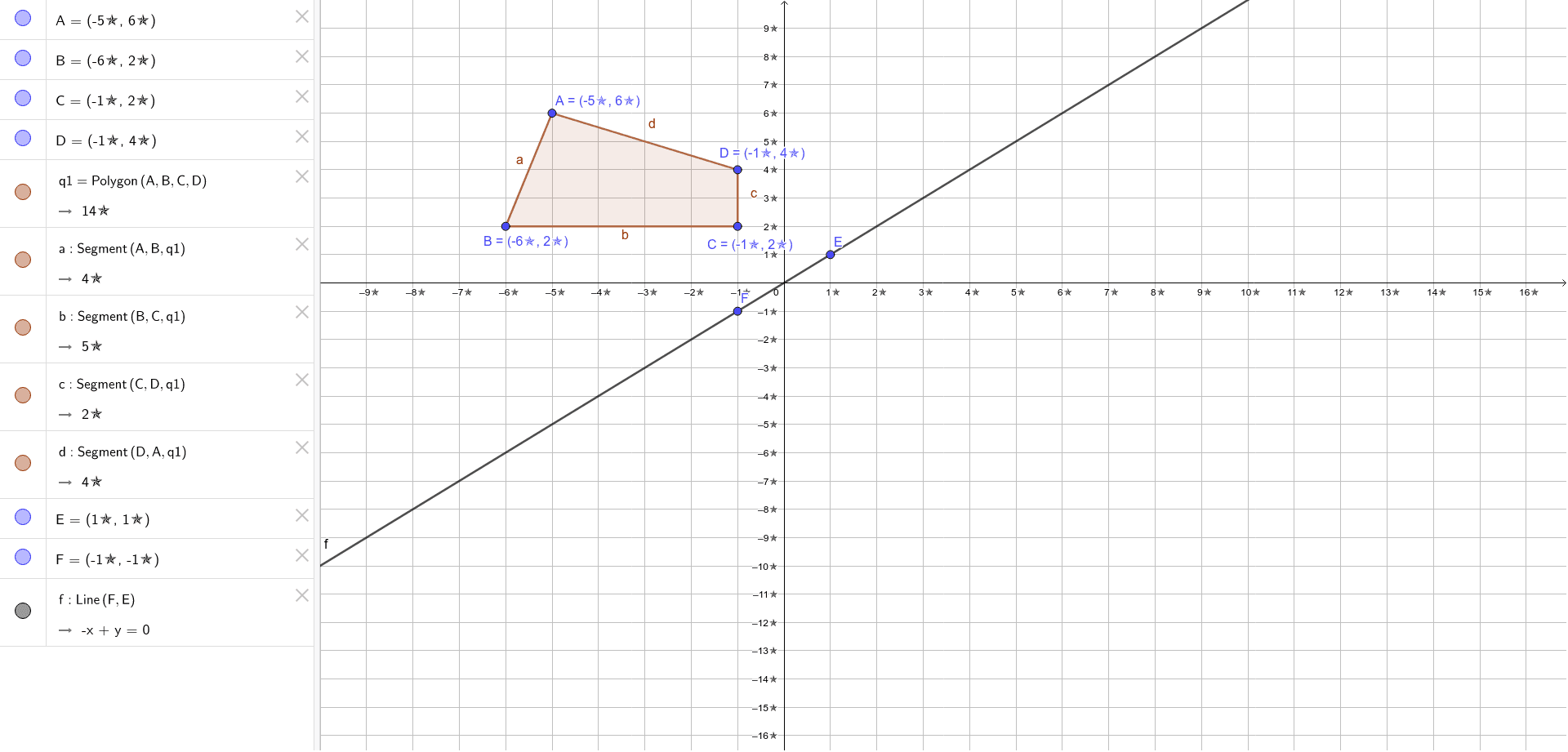



Reflection Across The Line Y X Geogebra



Reflecting Points Video Reflections Khan Academy




Picture Of Reflection Across Y Axis Reflection Math Math Reflection




Algebraic Representations Of Reflections
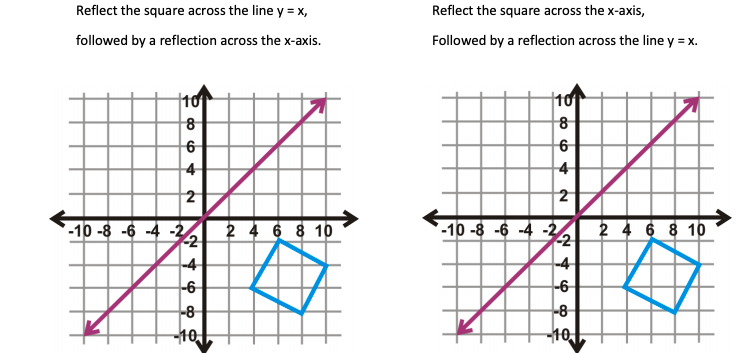



Solved Reflect The Square Across The Line Y X Followed By Chegg Com




Reflection Over Y 2 With Rule Educreations




Reflection Mathbitsnotebook A1 Ccss Math




Write The Coordinates Of The Vertices After A Reflection Across The Line Y X Brainly Com
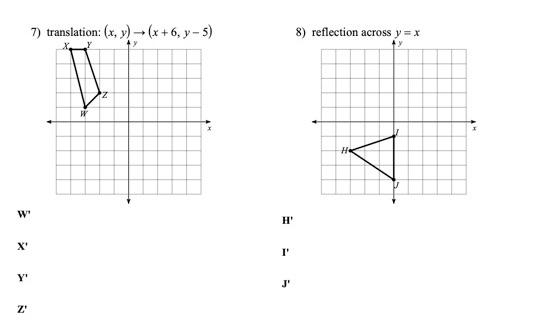



Solved 7 Translation X Y X 6 Y 5 8 Reflection Chegg Com




How Are We Studying Transformations Differently By Eureka Math Eureka Math Medium




Reflection Over The Line Y X Youtube



Reflection Across The Y Axis Math Functions Showme




D Reflection Across Y X Brainly Com




How To Reflect A Line Segment Across The X Axis Or Y Axis Geometry Study Com



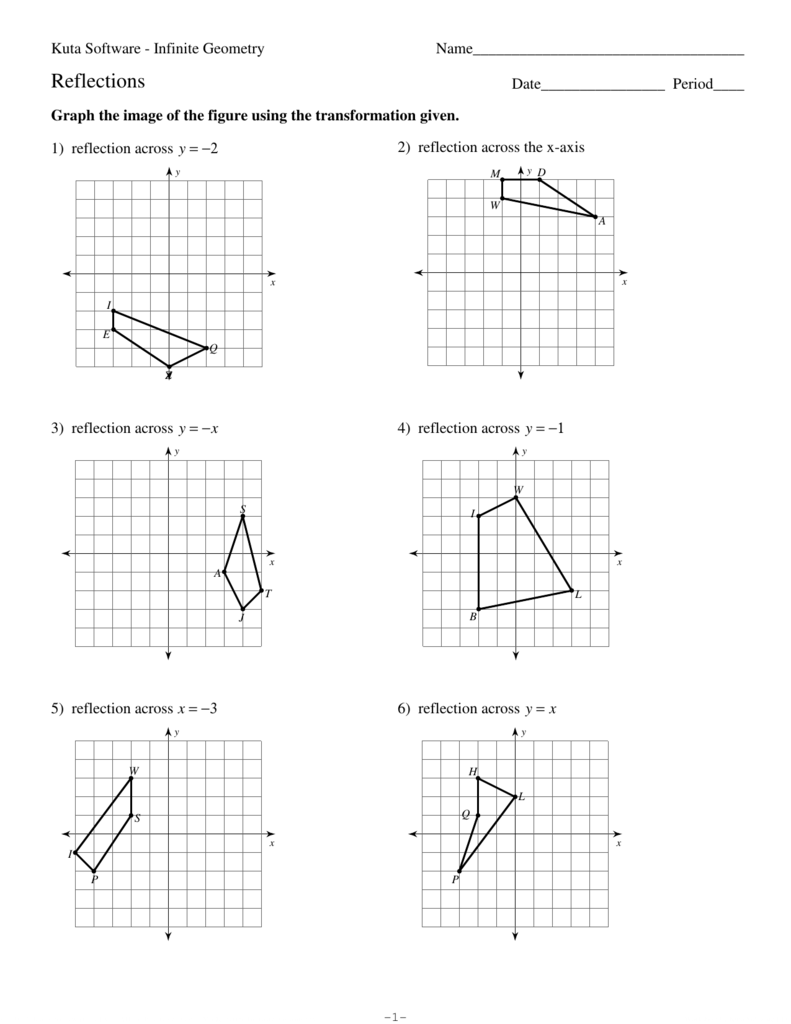
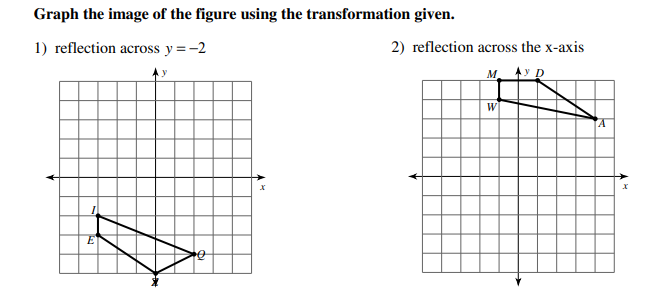
Reflections Kuta Software



Reflection Across



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative




Reflections Bright Star Schools



Reflection Over The Y X Line Youtube



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com
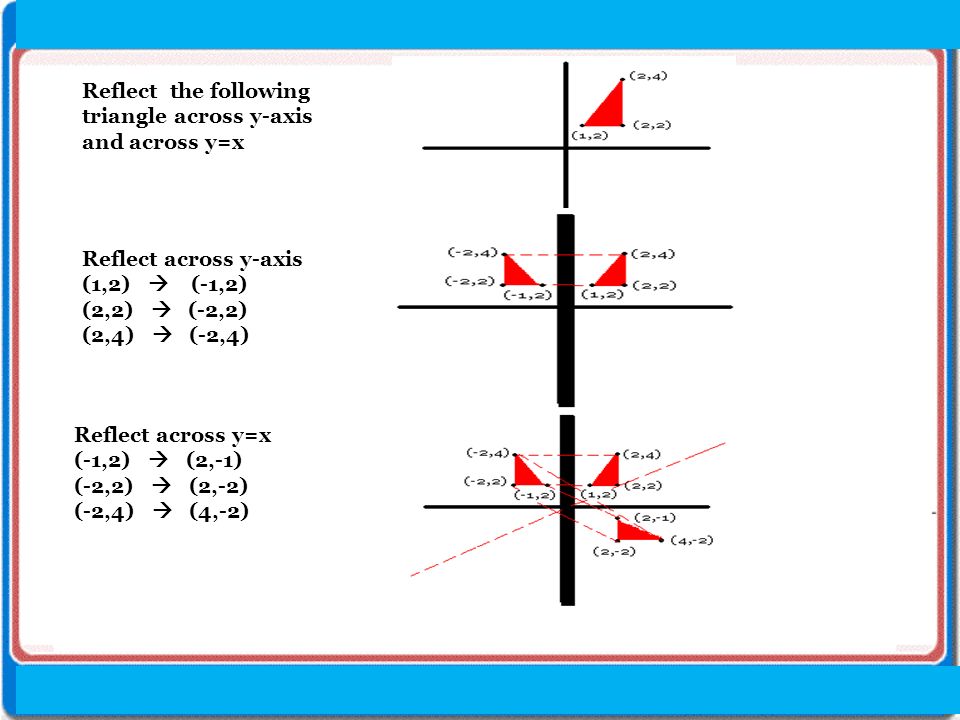



Reflections 30 Reflect Across Y X X Y Y X Reflect Across X Axis X Y X Y Reflect Across Y Axis X Y X Y Reflect Across Y X Reflect Across Ppt Download




4 2 Reflections Warm Up Maintaining Mathematical Proficiency Find The Measure Of Each Variable Justify Your Solution Ppt Download




Rules For Reflections Read Geometry Ck 12 Foundation



Biomath Transformation Of Graphs
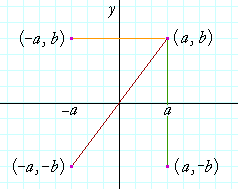



Reflections Of A Graph Topics In Precalculus
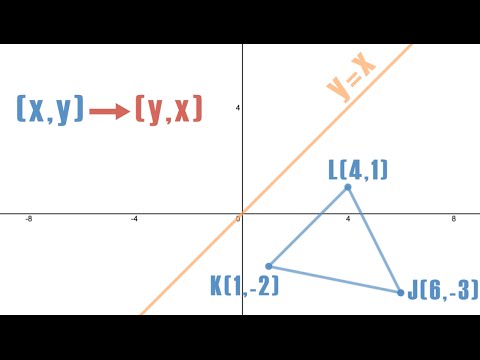



Reflection Across Y X Silent Solution Youtube
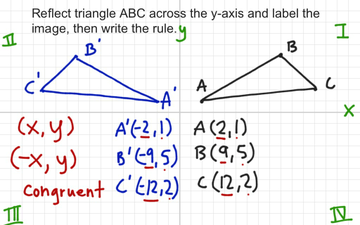



Reflection Across The Y Axis With Rule Educreations
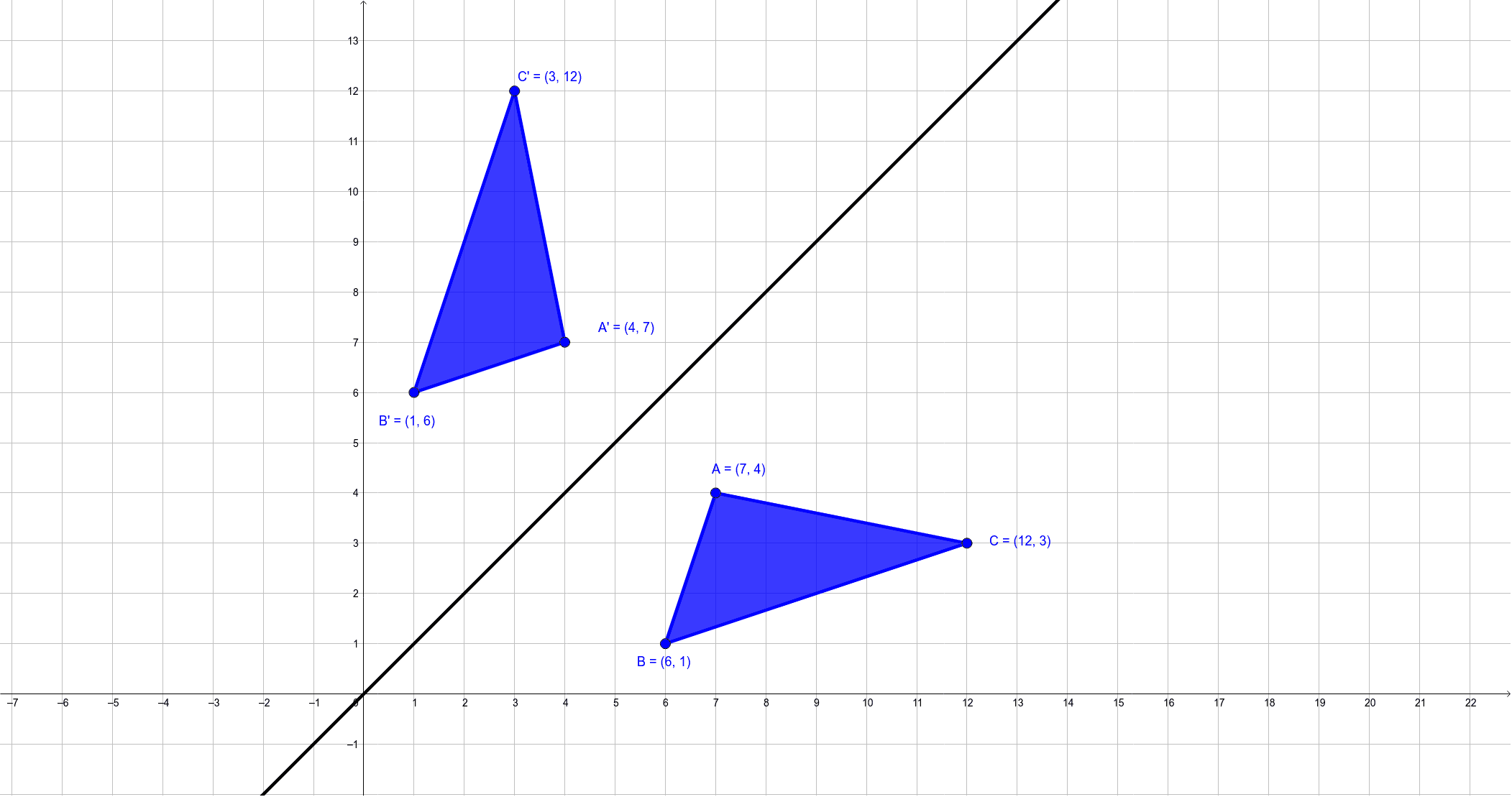



Reflection Across Y X Geogebra




Reflections How To Reflect A Point Reflect Point Across X Axis Y Axis And Other Lines Reflection Math 8th Grade Math Maths Activities Middle School



Biomath Transformation Of Graphs




Ex Reflect A Point About The X Axis Y Axis And The Origin Youtube



Reflections Ez Graphing
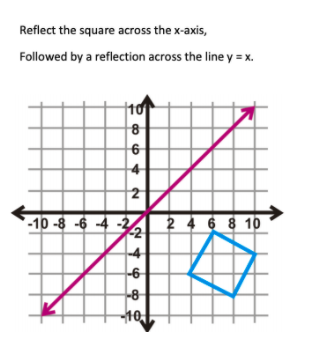



Solved Reflect The Square Across The X Axis Followed By A Chegg Com



Solved Which Glide Reflection Describes The Mapping Delta Chegg Com




Reflections




Reflections Across Y X And Y X Memory Match By Jstalling Tpt
コメント
コメントを投稿